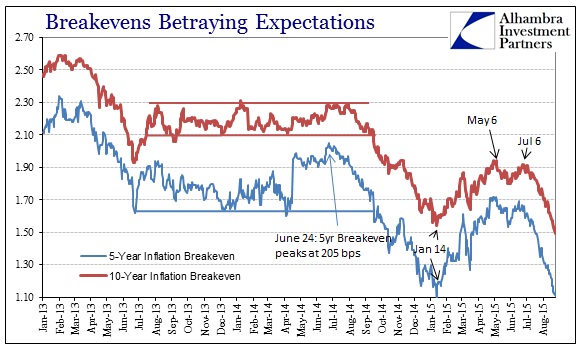
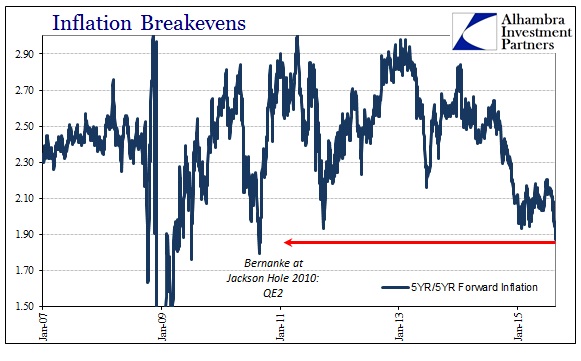
Lost in all the stock market focus is the renewed disaster being signaled across credit markets, “inflation” expectations in particular. Here oil prices and the “dollar’s” darkening intersect with credit and broad financial settings. Quietly, market-based measures of the anticipated future “inflation” path have crashed. Inflation breakevens in TIPS hedging were as low yesterday as the lowest point from January 14 in the 5-year; seriously lower at the 10s. Even the Fed’s preferred market measure of expectations, the 5-year/5-year forward inflation calculation, dropped to a low not seen since the highly unstable days exactly five years ago, just before Bernanke uttered QE2 to 2010 Jackson Hole.
It may all seem outwardly as just a minor inconvenience for the FOMC battling “market” conditions on almost every front, but this is not a small or insignificant deviation. The fact of this second “wave” of crashing destinies is confirming on several fronts, none of which are favorable to the continued (somehow) dominant monetary view. Starting in December, the crash in oil prices was not unnoticed but rather publicly set aside.
From Janet Yellen’s December 2014 press conference, in the prepared remarks:
Inflation has continued to run below the Committee’s 2 percent objective, and the recent sizable declines in oil prices will likely hold down overall inflation in the near term. But as the effects of these oil price declines and other transitory factors dissipate and as resource utilization continues to rise, the Committee expects inflation to move gradually back toward its objective. In making this forecast, the Committee is mindful of the recent declines in market-based measures of inflation compensation. At this point, the Committee views these movements as likely to prove transitory, and survey-based measures of longer-term inflation expectations have remained stable. [emphasis added]
That view in favor of “survey-based” measures to disregard market-based prices was linked in short-term money rates that described expected future economic conditions that might (or should) accompany both deviating paths. From the December 2014 Policy Statement itself:
A couple of participants remarked on the apparent disparity between market-based measures of expected future U.S. short-term interest rates and projections for short-term rates based on surveys or based on the median of federal funds rate projections in the SEP. One participant noted that very low term premiums in market-based measures might explain at least some portion of this gap. Another possibility was that market-based measures might be assigning considerable weight to less favorable outcomes for the U.S. economy in which the federal funds rate would remain low for quite some time or fall back to very low levels in the future, whereas the projections in the SEP report the paths for the federal funds rate that participants see as appropriate given their views of the most likely evolution of inflation and real activity. [emphasis added]
This December focus, such that it might have been, was not unwarranted given how much turmoil there was at that time; from ruble to oil and “dollar” again, there was at least the first rumbles (for orthodox views) of gathering trouble dead-set against all the happy sureties of the 2015 finish line seeming so provocatively in view. In the first few months of 2015, that survey-based view, as well as the modeled SEP, seemed at least more plausible as “negative” TIPS pressures and oil prices did appear almost transitory even if they never fully (or all that much) retraced the first wave of decline. In other words, there was hope in that it stopped, for the moment, getting appreciably worse in this context.
More recently, of course, the SEP has revealed a somewhat different tone even if still not quite synchronized with gathering market-based expectations into this second wave. As the last policy statement admitted, the committee no longer expects to find the economy at its “inflation” target before some time into 2018 now.
The staff’s forecast for inflation was revised down, particularly in the near term, as the decline in crude oil prices over the intermeeting period was expected to result in lower consumer energy prices. Although energy prices and non-oil import prices were expected to begin rising steadily next year, the staff continued to project that inflation would be below the Committee’s longer run objective of 2 percent over 2016 and 2017.
That is a huge failure for monetary policy that counts upon “inflation” not only as a standard for effectiveness but really as the transition between its efforts and actual economic growth (ridiculous as that theory may be, as they are finding out). Oil prices and inflation breakevens, as noted at the outset, have gotten much, much worse since even that point.
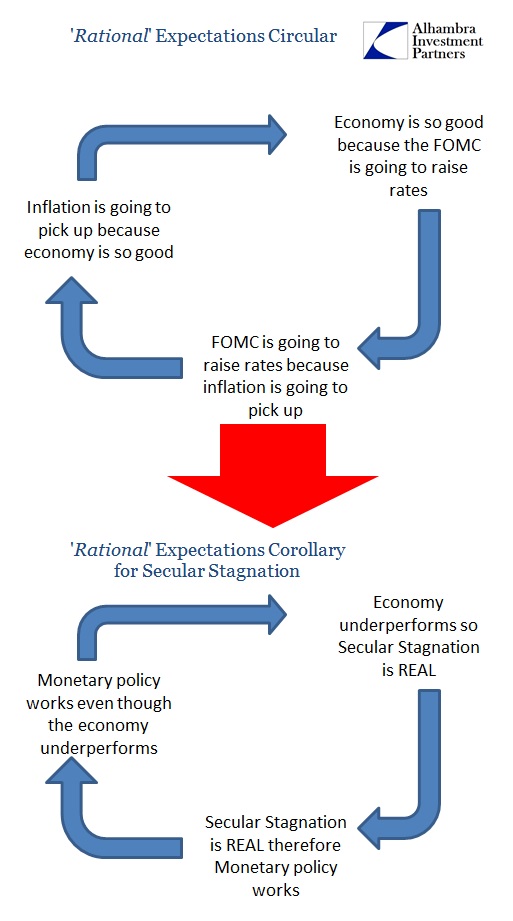
The meaning here is very plain, in that not only were the survey-based measures missing the true economic vane but the Fed’s models were, yet once again, completely useless in determining actual economic fortune. This isn’t really much of a surprise given the circular nature of those models, always assuming monetarism works because monetarism is assumed to work, but in this context it is quite more damning. Again, the FOMC has been planning and basing its actions upon the notion that “transitory” oil prices were an aberration to gaining economic function, “resource utilization” and “gradually moving back to target.” Being proved wrong here thus places the economy far, far more likely conforming to those market-based assumptions, including “less favorable outcomes for the US economy”; which is, in light of recent indications, quite the understatement.
It can no longer be transitory, which extrapolates nowhere good for monetary policy, orthodox economics and the actual global economy. The theme for several years now has been that “they don’t know what they are doing” and once more we find that proven by “unexpected” events that were perfectly predictable outside the orthodox bubble. The combined indications of bearish credit, the actual, wholesale “dollar” and other global proxies was rather clear in where all this was going. This renewed wave is just confirmation of that which was apparent all along; confirmation not just in reality but more so now, as time marches, in terms of potential depth.
There is, of course, the rational expectations component that begs for “inflation” expectations derived solely from reassuring or soothing “predictions” from these “best and brightest”, but what happens when you promise “transitory” and deliver instead quite more confirmation that you had it all wrong all along?
For a policy commitment the size of four QE’s and almost seven years of ZIRP intended for both “inflation” and then aggregate demand, there remains not just a shocking lack of either but a quite clear reversal of fortune that is proving this year disturbingly durable. We entered 2015 with the FOMC claiming there was no downside even where markets were at least unsure, taking some consideration of some serious probability in that direction. By this second wave, it is no longer just some serious probability, as the FOMC as much admits by its own inaction as set against those prior versions of its own expectations. By confirming that market prices were right and now with those getting to worse levels (including a time factor here, it is, after all, the end of August meaning continued investigation toward the downside reaches so far almost a year), what does that do to further extrapolations, eight months hence now lost?